Mating Sudoku

Natural Selection: the process whereby organisms better adapted to their environment tend to survive and produce more offspring.

Given that this age-old strategy of cultivating the fit and eliminating the weak has shaped everything from predatorial leopards to the complexity of human brains, it'd be safe to assume that it too could be employed to undertake menial tasks for lazy people, say, solve a sudoku for me. Right?

Well, let's give it a try!

Now the first step would be to understand the mechanisms of evolution. According to Wikipedia, there are 4 major aspects that concern the evolution of species in the natural world. 
1. Population
2. Sex & Recombination
3. Mutation
4. Selection

Step 1: Population


For natural selection and evolution to work, we first need to start with an initial population. In the case of my sudoku-solving quest, I will have to start with a randomized solution that fills up the sudoku puzzle. 

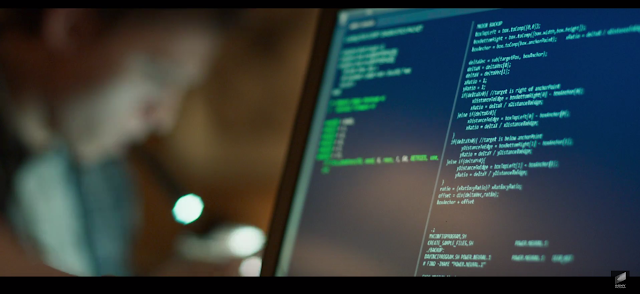
First, I load up a problem set as demonstrated to the left. Then, the program generates a list of 15 randomized solution, as shown below:

Alright, that fulfills the step one of evolution. As you can see from the solution above, there are many violations to the sudoku rule, such as repeating digits in the same row/column or in the same 3x3 tile. We need to start pairing these random solutions with each other to produce offsprings that fare better than their randomized parents.



Step 2: Sex & Recombination

Here comes the fun part. To decide which pairs of randomized solutions get to 'mate' with each other and produce combined results, I opted to learn from nature. As natural selection prefers organisms with higher fitness index, I had to introduce an artificially-conceived Fitness Index to differentiate between the population. 

This is how the fitness index is calculated:

TL;DR: I took the maximum fitness score (243) and subtract 1 for every time a tile violates the row/column/tile non-repetition rule. So a row with the digits 6,5,6,4,9,1,2,1,6 would lead to deduction of 3 scores due to repeating 6s and 1s

Whew. Now that we got that sorted, let's see just how fit our first generation of sudoku solutions are. 

A whopping 92/243! That's horrible, and as you can tell from how the numbers are arranged, there are so many errors and repetitions and digits across rows and columns.

Luckily, we don't have to panic yet. Despite starting off as blind and deaf unicellular organisms, we ended up faring pretty well after billion years of evolution. What we need is for our ancestors to have ample time and a lot of sex. A whole lot of 'em.

Cross-over mechanism:
1. Lottery to pick 2 sudoku-solutions for sexual reproduction(Chances are weighed by their Fitness Index)
2. Convert solution tables from both parties into lists of numbers. Then split the list of numbers at a randomized position and join the two lists together
3. Convert the joined list back into table form
4. A new baby is born

(For detailed understanding of the mechanism, refer to lines 41-67 in the source code)

Step 3: Mutation

If the population were left to intermix with each other, they will gradually converge into identical copies over time. Unless you are a fan of the dystopian clone-ridden future, we need to prevent this situation from occurring. If our sudoku-solutions were to converge too quickly, we will end up with suboptimal solutions with no room for improvement.

A working contingency plan, as demonstrated by nature, is to create random mutations. In nature, this happens because of DNA cloning errors. In the program, we artificially induce mutations on random tiles on the table.  

Note that mutation is not always good for the offspring. In 80% of the case, the mutation will lead to disastrous results, causing the offpsrings to shed off 20-30 fitness score. In the long run, mutation does lead to better diversity and more potential for growth.

 Step 4: Selection

This step is made easy for us. All sudoku solutions simply die off (or shall I say, executed) after each iteration. Their evolutionary success is judged solely by their reproductive ability, and that in turns is artificially determined by their Fitness Index. (Step 2)

With all four steps set in place, let's run our program!

As you can see, the average fitness and best fitness indexes are slowly climbing up after multiple generations of recombination and selection.

The process starts to slow down after 2-3 minutes as individuals of the population become more and more similar to each other. Here's the results after 4 hours of the repeated process, as taken from my previous run:



Pretty neat, eh? Admittedly, there's still room for improvements, as the solution hasn't reached the optimal solution of 240. For that to happen, better algorithms is needed, as my program hits a plateau at around the 200 region and never seemed to go over it.

Hope you enjoyed the read. All ideas and suggestions are greatly welcomed!

Source Code (Python): https://github.com/ImSandwich/AI-Code-Projects/blob/master/genetic.py

To test the code for yourself:
1. Download and install Python 3.6.x from https://www.python.org/downloads/
2. Download the source code
3. Open up Command Prompt
4. type cd [the folder you downloaded the source code to]
For example: C:\Users\User\Desktop\Code Projects\
5. type python genetic.py
6. Insert the desired population size (Recommended: 15)
7. Insert the desired mutation rate (Recommended: 0.04)
8. Insert the desired cutoff  (Recommended: 60, this is the minimum fitness a solution must have to be considered for survival)
9. Insert the desired scatter rate (Recommended: 0.15, this is a simulation of natural disasters that will occur leading to random selection of population)
10. Let it run, set back and enjoy =)

Imitation Game

Think of a number in your head. It could be anything from 0-9. Got it? Good.

Now let me guess what number it is.

First, I'll present you with ten random numbers. They are 3,3,1,4,9,7,8,4,3,1

Did the number on your mind appear in the list? Shout out '1' if it did!
It didn't? Oh well, reply with a '0' instead then.

Let's take a number for demonstration. We'll go with 5 as it didn't appear on the list. In accordance to the rule, at no time should I reveal the number on my mind, but instead let my computer figure it out on its own by feeding it '1's (if my numbers appeared in abundance) or '0's (if it did not)

I chose to input 0 on the first entry as my desired number did not appear on the list. Immediately on the second list we see the number '5' popping up.


By encouraging the computer with '1's when the number 5 is in abundance, it took the hint and increased its preference towards the number

The dominant guesses are now between 4 and 5


4s seems to slowly overtake 5s, so I fed it with a '0' as I am not satisfied with the computer's divided guess. On the following list, we can see the computer went with the number 5.




Slowly, by rewarding/punishing my computers with 1s(which it likes) and 0s(which it tries to avoid), it made out my intention and guessed the number 5.

Voila! A program that knows what's on your mind. Granted it is not the brightest at the game, and requires an average 15-20 inputs to arrive at an accurate guess, but nevertheless this simple app demonstrated an inherent ability to learn and adapt to the user's input.

Here's my goal: To keep the number of guesses down to 5-10. I'll keep you posted when I stumble upon an algorithm that allows for that level of quick learning.

Source Code (Python): https://github.com/ImSandwich/AI-Code-Projects/blob/master/learning_agent.py

To test the code for yourself, simply:
1. Download and install Python 3.6.x from https://www.python.org/downloads/
2. Download the source code
3. Open up Command Prompt
4. type cd [the folder you downloaded the source code to]
For example: C:\Users\User\Desktop\Code Projects\
5. type python learning_agent.py

Enjoy! All feedback and suggestions for improvement is greatly welcomed =) Peace out.

Animation stuff

So today I was bored. I just finished Season 2 of Broadchurch and had no idea what to do. So I decided to try my hand at animation. I found this really good tutorial over here.
https://design.tutsplus.com/series/animation-for-beginners--cms-923
 More specifically I went into the character walking part of the tutorial.

Now while drawing, I realised I didn't have a way to see how my animation turned out.

So I hacked away a nice little program in C# Winforms to view it.

I dubbed it "AnimationHelper". It's fairly basic without much features, but also very simple to use. Zip up all the image files (png only;it's by design, I hate all other file formats) of the animation and load that into the program, either through the Open File button or through Drag N' Drop. The default is 1 frame per second which can be adjusted, and I have a pause/play button.

That's basically all there is. Not even a "Developer" section attributing myself as the creator, or loading directly from psd/xcf files (Photoshop and Gimp respectively),or adjusting the position,or spritesheet adjusting, or basic editing, or exporting it as a video. None of that fancy stuff.

But it got the job done nicely, and I liked stuff I made myself which I can trust.

Side-thought : The code was hacked together so badly I'm not sure I can even trust my own code.....The Irony.

If you're looking to use something like this and are looking for a Download Link, Let me reassure you I will definitely not release this. It's an abomination. It's a single-platform only hacked together code in a couple hours by someone who barely even knows C#. The only good thing I could say about it is its simplicity.

If you want something like this I suggest this place (I am not sponsored, this is not mine)

https://www.leshylabs.com/apps/spriteSheetAnimator/

It's written in HTML5 by the way, so if you're worried about not having a connection when you want to use it, Just hit Ctrl+S (Or whatever the Apple Equivalent is...) on the page.

Well.... back to drawing instead of procrastinating at my terrible art skills and making a program for no reason.

You Won't BELIEVE what I found in the new Spiderman : Homecoming trailer!

Note that I like to pander about, talking about whatever comes to mind, if you want to get straight to the analysis scroll down till you see the code.

I found decorative computer code. There, now send me an angry comment for the clickbait and be on your way, Internet stranger.
(But pls remember to tweet how angry you are and don't forget to link this and Google Plus this (I don't judge you for using that) and Facebook and send this to all your friends! Email if you have too! Or -gasp- talk to your friends about this!)
....
plz
....
 i hvae no raeders
....
I am broken inside
...
 :'(
....

Anyway here's Spidey's suit given to him by Tony

(Image courtesy of Sony, screencapped from the Youtube trailer, (98027 views as of writing) all of these are from there, don't sue me please :(  
 I'm also pretty sure it's legal for me to use this under fair use as long as I don't use it in it's entirety for educational purposes or something like that, so there's that. Sorry for rambling, readers. Wait I thought I have no readers?)

Looks pretty cool, apparently the red and blue isn't painted on but is emitted through the suit. Handy
for changing colour schemes and logos in the future without having to come up with the old "Upgraded suit" cliche.

Looks like the entire suit is a circuit. And guess what, it's programmable too!



Anyways here is the code, presumably in-universe written by Tony Stark. I believe this is the first time we see his actual code on-screen in the MCU.



So, either Tony left some code for Spidey to play with (but he blocked out most of it with "The Training Wheel Protocol", wow Tony. Just. Wow.).

I heavily suspect there is more code at the top and bottom, but the screen is scrolled somewhere in the middle of the code. That also explains the "boxAnchor + offset" meaningless code at the bottom, it's not fully displayed and maybe it's a typo or something.

If someone could identify the language used (assuming it's a real language), I would appreciate it. Right now my theory is....Javascript? I honestly have no clue.

So let's take a look at the code. I've written down for you, the non-existent reader's, convenience

MODEM BACKUP
boxTopLeft = box.toComp([0,0]);
boxBottomRight = box.toComp([box.width,box.height]);
boxAnchor = box.toComp(box.anchorPoint); xRatio = deltaX/distanceEdge;

deltaVec = sub(targetPos,boxAnchor);
deltaX = deltaVec[0];
deltaY = deltaVex[1];
xRatio = 1;
yRatio = 1;

if (deltaX>0)
{
    //target is right of anchorPoint
    xDistanceToEdge = boxTopLeft[0] - boxAnchor[0];
    xRatio = deltaX / xDistanceToEdge;
}

else if (deltaX<0)
{
    xDistanceToEdge = boxTopLeft[0] - boxAnchor[0];
    xRatio = deltaX / xDistanceToEdge;
}

if (deltaY>0)
{
    //target is below anchorPoint
    yDistanceToEdge = boxBottomRight[1] - boxAnchor[1];
    yRatio = deltaY / yDistanceToEdge;
}

else if (deltaY<0)
{
    yDistanceToEdge = boxTopLeft[1] - boxAnchor[1];
    yRatio = deltaY / yDistanceToEdge;
}

ratio = (xRatio>yRatio) ? xRatio:yRatio;
offset = div(deltaVec,ratio);
boxAnchor + offset

.;
MYCONFIGPROGRAM,SH
CREATE_SAMPLE_FILES,SH            BLURRY
./BACKUP:
DAVINCIPROGRAM.SH POWER.NEURAL.;     BLURRY
# FIND -INAME "POWER.NEURAL.1"

So yeah. Sorry I can't read the super blurred out section on the left.
Tony Stark has some really buggy code.By the way if you want, look at the picture you can see his style of writing code, the positioning of brackets and the like. Just an interesting observation, a man's style of writing is as expressive as his walking gait and personality in my opinion.

So at first glance, I think it's definitely something to do with geometry as evidenced by all the coordinates of Xs and Ys and Vectors.

Now I was too lazy to actually read the code, so I made up 2 hypotheses as to what it could be

1. Detection for where to shoot web (it was mentioned there was 576 possible web shooter combinations in the trailer)
2. Spidey's Heads Up Display GUI

Yes. Spiderman does have a HUD like Iron Man.



Honestly I like him better independent. Ah well it's a kick-ass cool suit.

I ruled out the first theory because  it seemed to simple for pattern recognition and the like.For some daft reason, I also ruled it out because of the lack of a 'z' coordinate in the real world. Only a little later did I realise that cameras on the suit (if there are any) would capture in 2d hence the lack of a z coordinate.

So it's likely to be used somewhere in Spiderman's HUD.

But what is it actually?

it seems to have an input a deltaVec 2d coordinate, a bounding box which I assume contains the deltaVec (it makes sense), and the target 2d coordinate I assume is away from the box.


(Yeah, sorry I didn't have my tablet at the time and now I'm too lazy)

First off it calculates the ratio between a) distance between the delta and the side of the box (in the direction of the target) b) distance between the input and the target.
Rinse and repeat for all possible cases for both x and y (4 cases, calculate X for left and right, calculate Y for up and down).

Note within a note : It may seem there are cleaner ways to do this with less code (i.e: taking the absolute value only so that eliminates
the need for if statements), but after some thinking, the code provided is actually the most readable way of doing this.

It seems to target the higher ratio first, that is, the one with a further distance to target and smaller distance to side of box,
then divide the delta vector by that "bigger" ratio.
What I don't get is why it chooses the "bigger" ratio for dividing *both* x and y coordinates in the vector. it would make more sense
for

offset = div(deltaVec[0],xRatio);
offset = div(deltaVec[1],yRatio);

where deltaVec[0] and deltaVec[1] are the x and y coordinate respectively.
THIS would have created a still weird but totally slightly more logical normalization.
No idea why it does what it does. Hit me up with a comment if you have a theory and definitely contact me if you managed crack the whole thing wide open and figured out what it does.

For the curious wondering what a normalization is, Wolfram Alpha defines it as so:

The normalized vector of x is a vector in the same direction but with norm (length) 1.

 This is used in conjunction with targetCoordinates-playerCoordinates to get the direction vector to move and multiply that with a speed float instead to control the speed. So a player from (0,0) to enemy (3,3) would give (3-0,3-0) and thus (3,3) as the direction (northeast). So That's is essentially moving (1,1) at a speed of 3 units per second. What normalising does is take the (3,3) and makes it into a (1,1) but the ratios must still be the same (3:3 is equal to 1:1)

Yes I understand the so-called "normalization"  does not have a unit length of 1. I'm still fairly sure the ratios are still the same though. I have no idea why or how they Tony did it like this. Genius level code obfuscation?

Hit me up with a comment if I got normalization completely wrong.
Be as harsh as you want, I have no emotions.

Hit me up with a comment if I got spelling errors.
Be as harsh as you want, I have no emotions.

Hit me up with a comment if you want to talk.
Be as harsh as you want, I have no emotions.

Side-thoughts:
The script "DAVINCIPROGRAM.SH POWER.NEURAL.;" seems to indicate a shell script named after Leonardo Da Vinci. The word Neural, which I first read as Neutral (assuming like as in Live, Neutral, Earth/Ground) but upon reinspection it is most definitely Neural. This word, along with the word Da Vinci, leads me to believe that this is a shell script for activating a Artificial Neural Network (Artificial Intelligence) for pattern finding in the real world through cameras to estimate where best to shoot those webs. Keep in mind this is a long shot and just a not-very-useful movie-wise theory which will likely never get verified (or debuked).

What the heck is "xRatio = deltaX/distanceEdge;" for?
xRatio gets reassigned a few lines later without ever being used.
Perhaps out of the reach of the screen we could not see it was being used for something though.
Why that weird ugly style of coding for someone of the likes of Tony Stark? I do not know.

All in all I was impressed with how they handled the code in the trailer. It might not be the perfect code, but honestly it's good enough for just a quick glance even by a coder.It visually feels interesting while not falling into the trope of having animated ASCII art and colourful GUIS all over the place with an deliberately attention-seeking "Look at me I'm a computer genius look at these random 0s and 1s and scrolling of texts in a green font" type of code. It even seems to be doing something, something related to the suit without ever mentioning "Spider" or something in the code, though I still for the life of me do not know what that something is.

But then again, fools know nothing.
(that was supposed to be a profound endin-

New Direction

Hello! I'm sure you're glad to learn that this blog isn't dead yet =)

There we go, a notification to remind you that there's something new in store. so... what's the message?

Basically, I've come up a new idea for an app, thus explaining the title, as I would be gearing my learning experience towards realizing this new app idea that I've conceived. What's it about? Well, that part would unfortunately have to remain a mystery for now, but it is safe to say that the mechanism of Notification plays a big role in this app(which is also why my very first priority was to learn how to code a phone notification).

That's about it for this update, really. I admit guiltily that I haven't really been spending as much time on programming as I should, so hopefully this post serves as a reminder for myself to set the wheels rolling and devote more time in this endeavor of mine.

After all that's what a notification is for, right? A reminder.

Baby steps

Alright, I'm officially a beginner developer now! Looking at that fancy emulator booting up to my simple program, I'm already thrilled to my bones with excitement. This also marks my transition into Javaprogramming instead of my old tool C++, as android studio provides a native support for java.

Alrighty, first things first. My primary objective today shall be to run a makeshift app on my smartphone. Nice and simple, ey?

--- 1.5 hours of excruciating troubleshooting later ---



I've finally managed to install adb drivers on my computer! Gosh.

"file path not accessible..." "phone not detected..." tons of unexpected issues seem to jump out of thin air to dissuade me of my very first attempt, and the worst of all - I can't find anyone else online with the same problem as me! I'm forced to go the hard way, digging through forums after forums, restarting my computer a good number of times and downloading strange files on the Internet with only one thing in mind: One of these oddballs is going to fix my problem.

But of course, bad spell doesn't last forever, and eventually my Android Studio reported a build success and all the files begin compiling. I held my breath for a good dozen of seconds, then voila! My phone screen lights up with a blank screen and a lonely textbook that says 'Name'. Almost in an instant the voice in my head telling me that 'I'm wasting this whole night on nothing' was pulverized, and I'm left with a heartfelt glee.

This is gonna be fun.

New Beginnings - Android App Development

So me and my friend decided to embark on a learning journey to hone our programming skills and I'm very excited getting into this big ambitious project. Since this is my very first post on the site, I'll start off by introducing myself! Hooray!

My online alias is ImSandwich, and I'm avid sandwich eater. My favorite combination of food? Ice cream sandwich, of course! For that very reason, I am a fan of Android(referencing to OS Android 4.0, "Ice Cream Sandwich"). Sorry, Apple! You're still my third favorite fruit though ~(^.^)~

With that in mind, I settled on spending the next half year in pursuit of mobile phone app dev. I have toyed around with Visual Basic, C# and C++ programming on Visual Studio IDE before, and now I can't wait to extend my reach by delving into Android app development. Let's take a look at my progress as of right now...

Buckle up folks, because a new guy is coming to town!

As you can see, I'm already making baby steps towards my dream, and I promise you I'll keep you updated on every niche of my progress, keeping no truths hidden about the life of a school-teenager trying to get his hands on the computer world. To spice things up, my friend and I have challenged each other to report our individual progress once every 3 days, so fear not that this blog will ever go silent! We might want to come up with punishment ideas for whomever breaks this rule, but in the meantime, I should get started with all dem Youtube tutorials!

Ciao